The norm of a complex number \(z=x+yi\) is
\[\CAbs{z} = \sqrt{x^2 + y^2}\]The theorem of Pythagoras tells us that \(\CAbs{z}\) is the distance of \(z\) from \(0\):
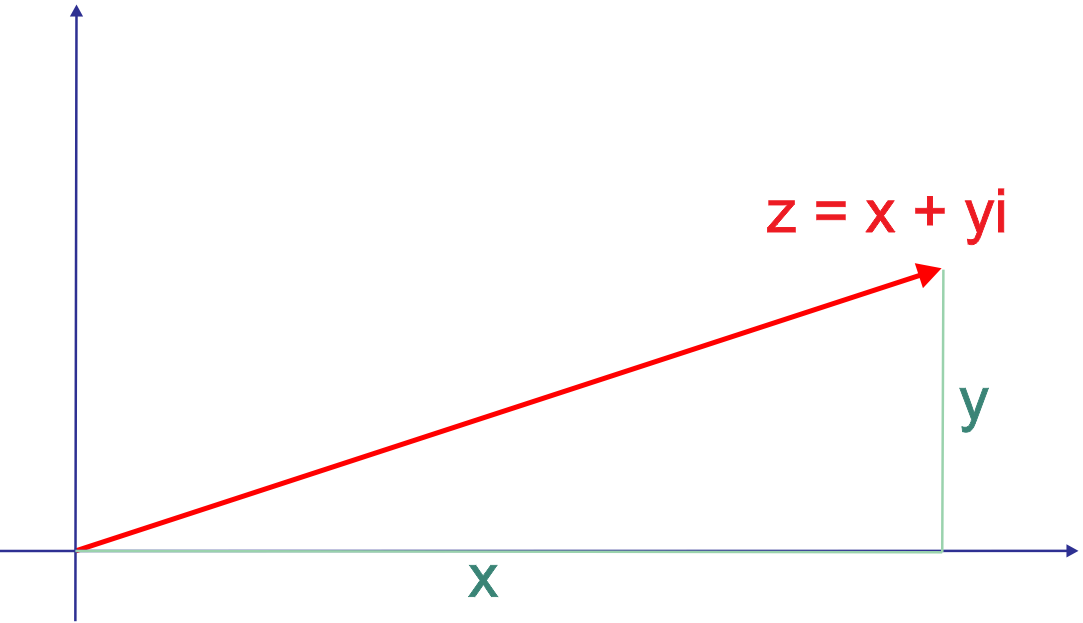
Note that in the special case where \(z=x+0i\) is a real number, the complex norm operation just returns the absolute value of \(x:\)
\[\CAbs{z} = \sqrt{x^2} = \Abs{x}\]