The inverse of a complex number \(z=x+yi\) can be found in two steps
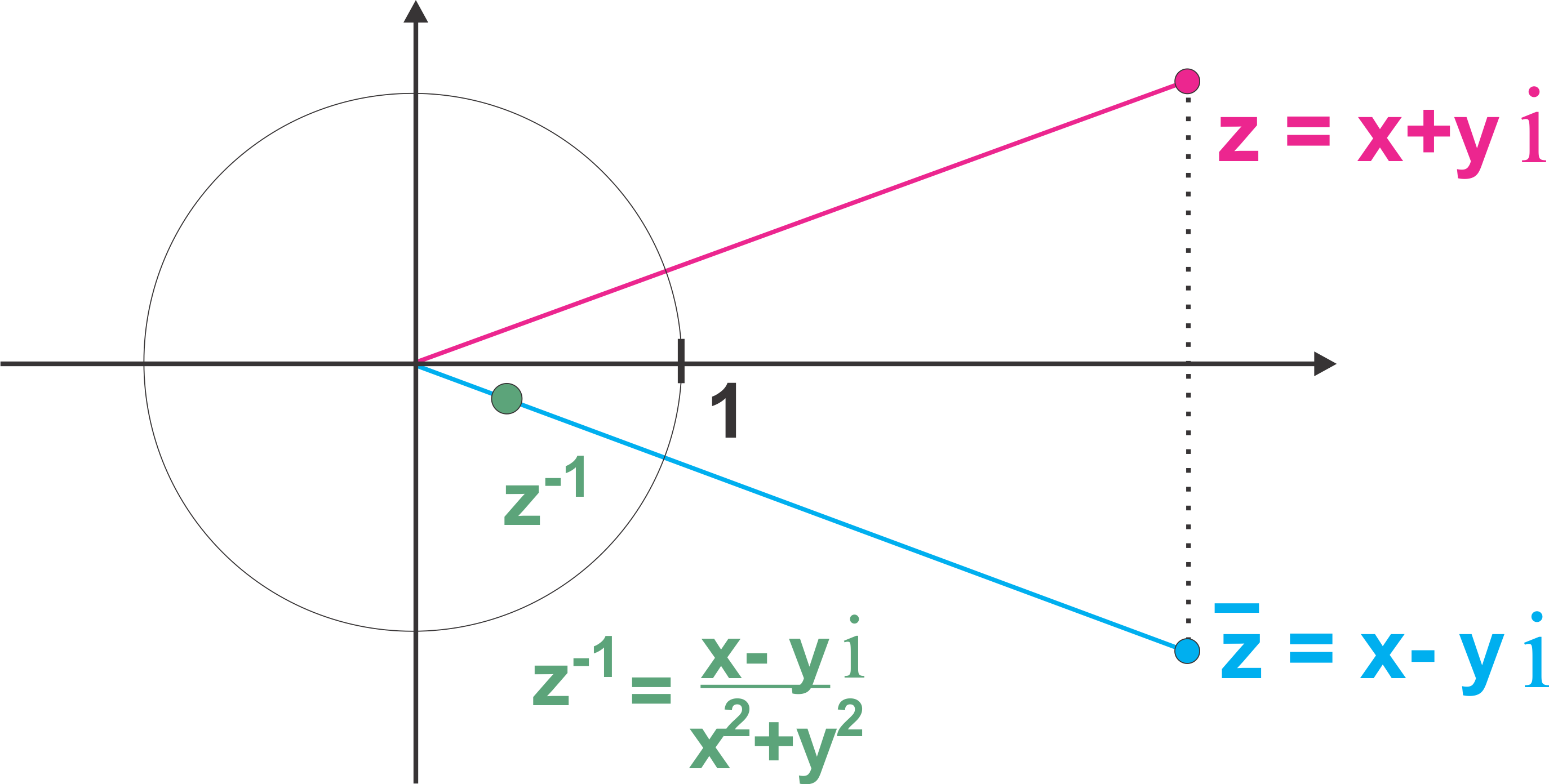
- Find the conjugate \(\CCnjgt{z} = x -yi\). This amounts to reflecting \(z\) over the \(x\)-axis.
- Rescale \(\CCnjgt{z}\) by the factor \(z\CCnjgt{z} = \CAbs{z}^2\). This amounts to reflecting \(\CCnjgt{z}\) over the unit circle. Or, in other words, if \(z\) and \(\CCnjgt{z}\) have distance \(r\) from the origin, then \(z^{-1}\) has distance \(r/r^2=1/r\) from the origin.