The idea behind polar coordinates is to express the location of a point \(z=x+yi\) in the plane \(\CNr\) in terms of its angle from the positive \(x\)-axis and its distance from the origin.
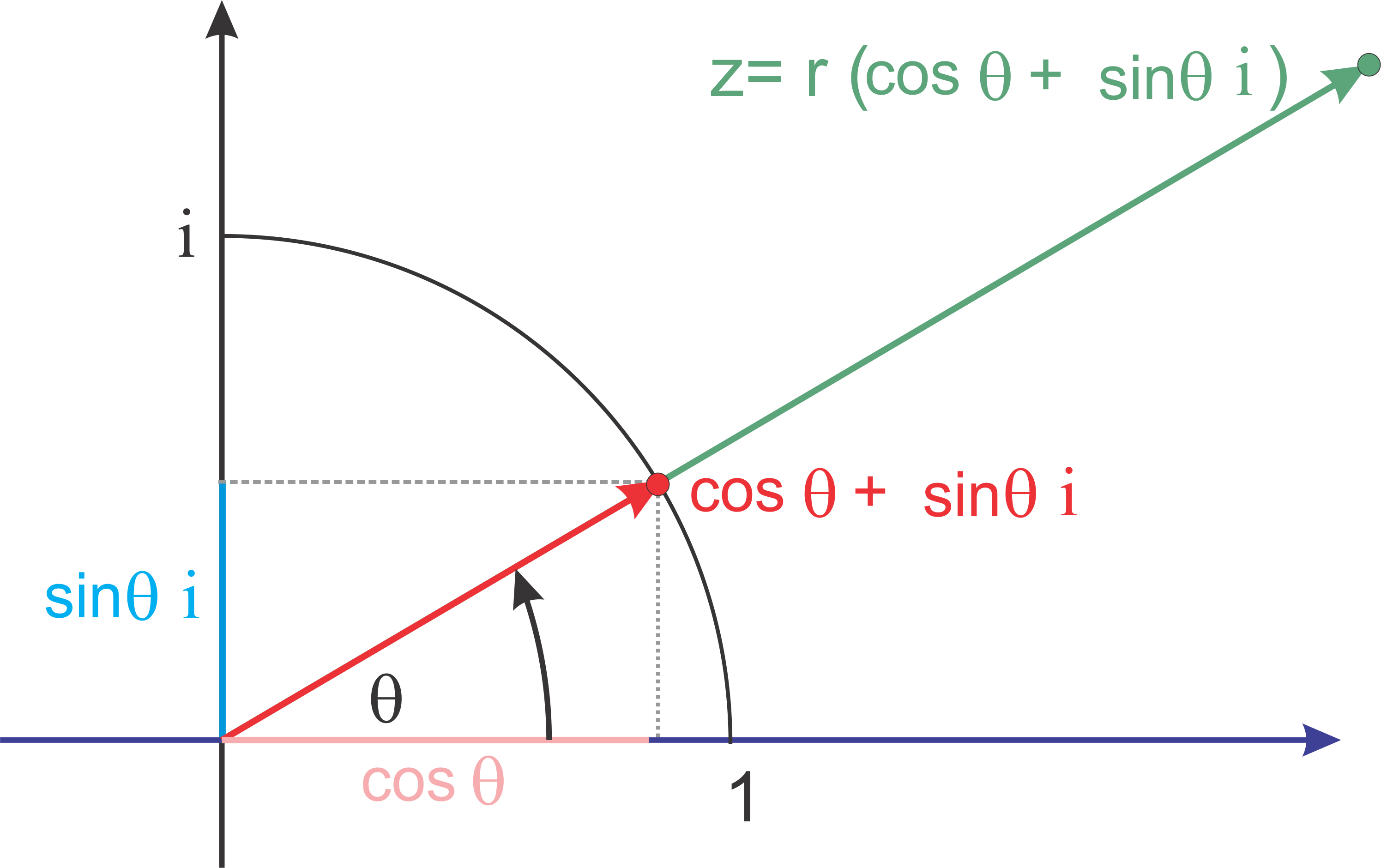
Here \(r=\CAbs{z}\) gives the distance of \(z\) from the origin. This means that
\[z=x+yi = r\cos\theta\ +\ r\sin\theta\cdot i\]For example,
| \(1+i\) | \(=\) | \(\sqrt{2}\cdot \left( \cos\dfrac{\pi}{4} + \sin\dfrac{\pi}{4}\cdot i\right)\) |
| \(4i\) | \(=\) | \(4\left( \cos \dfrac{\pi}{2} + \sin\dfrac{\pi}{2}\cdot i\right)\) |
| \(-2-i\) | \(=\) | \(\sqrt{5}\cdot (\cos\theta + \sin\theta\cdot i)\) |
where \(\theta\) is an angle such that
\[\cos\theta = -\dfrac{2}{\sqrt{5}}\quad \text{and}\quad \sin\theta = -\dfrac{1}{\sqrt{5}}\]