In the picture below, the hyperplane \(H\) is the line passing through \(P\). We wish to find the distance from \(Q\) to \(H\).

To this end we express the position vector \(\Vect{q}\) of \(Q\) as
| \(\Vect{q}\) | \(=\) | \(\Vect{p}\ +\ (\Vect{q}-\Vect{p})\) |
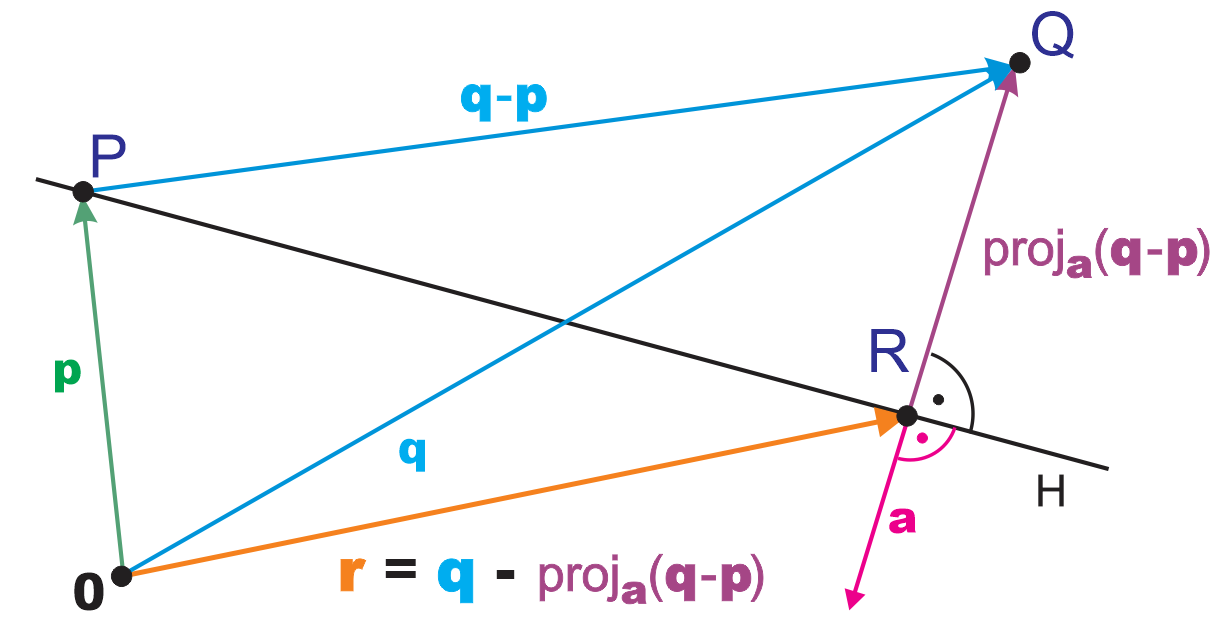
Projecting \((\Vect{q}-\Vect{p})\) along the normal vector \(\Vect{a}\) to \(H\) yields the shortest possible vector \(\OrthoPrjctnOf{\Vect{a}}{\Vect{q}-\Vect{p}}\) which joins \(H\) to \(Q\). Therefore
| \(\Vect{r}\) | \(\DefEq\) | \(\Vect{q}\ -\ \OrthoPrjctnOf{\Vect{a}}{\Vect{q}-\Vect{p}}\) |
is the position vector of \(R\), the point on \(H\) which looks closest to \(Q\). – Why is it truly closest to \(Q\)? Well, if \(X\) is arbitrary on \(H\), then the arrow \(\Arrow{X}{Q}\) is the hypotenuse of a right triangle which has \(\Arrow{R}{Q}\) as one of its sides. So \(\Dstnc{X}{Q}\geq \Dstnc{R}{Q}\).
Finally the distance of \(Q\) from \(H\) is
| \(\Dstnc{H}{Q}\) | \(=\) | \(\Dstnc{R}{Q}\) |
| \(\) | \(=\) | \(\Norm{ \OrthoPrjctnOf{\Vect{a}}{\Vect{q}-\Vect{p}} }\) |
| \(\) | \(=\) | \(\Abs{ \DotPr{ (\Vect{q}-\Vect{p}) }{ \dfrac{\Vect{a}}{\Norm{ \Vect{a} } } } }\) |
| \(\) | \(=\) | \(\dfrac{ \DotPr{ (\Vect{q}-\Vect{p}) }{ \Vect{a} } }{ \Norm{ \Vect{a} } }\) |
So this is where the distance formula for a point from a hyperplane comes from.