Projection of a Vector onto a Line – Illustration

The projection of a vector \(\Vect{x}\) in \(\RNrSpc{n}\) onto the line through the origin in the direction of a nonzero vector \(\Vect{y}\) is defined as

\[\OrthoPrjctn{{L}{\Vect{x}} = \dfrac{ \DotPr{\Vect{x}}{\Vect{y}} }{ \DotPr{\Vect{y}}{\Vect{y}} } \cdot \Vect{y}\]

The effect of this projection may be visualized as follows

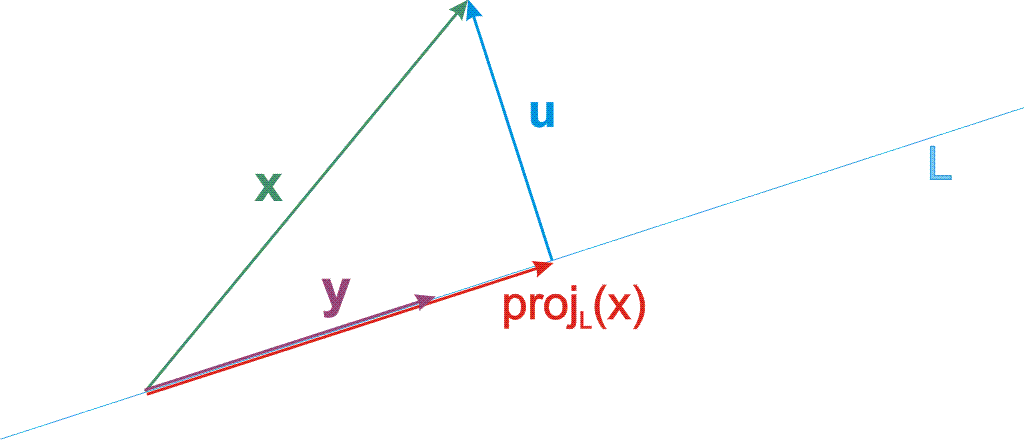
Shine a light vertically onto the line \(L\). The shadow of \(\Vect{x}\) is the projection of \(\Vect{x}\) onto \(L\). Crucial properties of this projection are:

• \(\OrthoPrjctn{L}{\Vect{x}}\) is parallel to the direction vector \(\Vect{y}\) of \(L\).
• The difference vector \(\Vect{u} \DefEq \Vect{x} - \OrthoPrjctn{L}{\Vect{x}}\) is perpendicular to \(L\) and to \(\Vect{y}\).