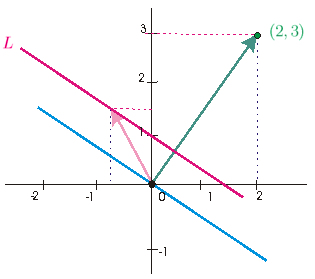Hyperplane – Illustration

Here we illustrate a hyperplane in \(\RNrSpc{2}\) or in \(\RNrSpc{3}\).

A hyperplane in \(\RNrSpc{2}\) is just a line

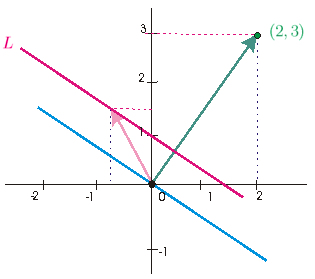
In the picture above, the blue line is the hyperspace which is perpendicular to the green normal vector. The red line \(L\) is a hyperplane. It results from parallel translating the blue hyperspace.

An equation for the hyperspace (blue) is

\[\DotPr{(2,3)}{(x,y)} = 2x + 3y = 0\]

An equation for the hyperplane (red) is

\(2x+3y\)	\(=\)	\(3\)
\(\DotPr{ (2,3) }{(x,y)}\)	\(=\)	\(\DotPr{ (2,3) }{ (0,1) }\)

A hyperplane in \(\RNrSpc{3}\) is just a plane in the usual sense

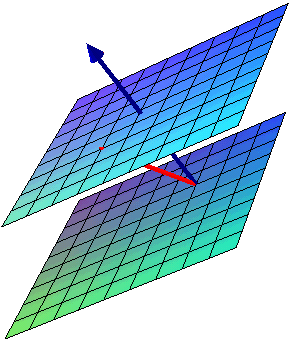
In the picture above, the planes are hyperplanes in 3-space. The tail of the two arrows is supposed to be at the origin. So the lower hyperplane passes through the origin and, hence, is even a hyperspace. In general, we characterize the location of a hyperplane by specifying a vector \(\Vect{a}\) (blue) perpendicular to it and by specifying a point on it (the tip of the red arrow). Alternatively, we can think of a hyperplane as being obtained by parallel translating the hyperspace which is perpendicular to \(\Vect{a}\) off of the origin by a suitable vector (red).

If \(\Vect{a} = (a,b,c)\), then an equation for the hyperspace

\[\DotPr{(a,b,c)}{(x,y,z)} = ax + by + cz = 0\]

If the hyperplane passes through the point \(P(p,q,r)\) (with red position vector), then an equation for the hyperplane is

\(ax + by + cz\)	\(=\)	\(ap+bq+cr\)
\(\DotPr{(a,b,c)}{(x,y,z)}\)	\(=\)	\(\DotPr{(a,b,c)}{(p,q,r)}\)