We think of an arrow in \(\RNrSpc{n}\) as exactly what the word suggests: a perfectly straight object with a tail and a tip. Thus the location of an arrow in space is determined by two points, namely
- a point, say \(P\), which marks the tail of the arrow,
- a point, say \(Q\), which marks the tip of the arrow
We write \(\Arrow{P}{Q}\) for the arrow which has its tail at \(P\) and its tip at \(Q\). – The picture below shows three such arrows.
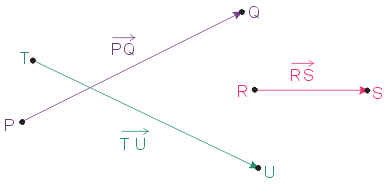
For example, the pink horizontal arrow on the right has its tail at a point named \(R\), and it has its tip at a point named \(S\). So we write \(\Arrow{R}{S}\) for the arrow joining \(R\) to \(S\). Similarly,
- \(\Arrow{P}{Q}\) denotes the arrow joining the point \(P\) to the point \(Q\).
- \(\Arrow{T}{U}\) denotes the arrow joining the point \(T\) to the point \(U\).