Example
The linear combinations of a single vector \(\Vect{x}\) consist of all vectors of the form \(t\cdot \Vect{x}\), where \(t\) in \(\RNr\) is arbitrary. – The graphic below shows some linear combinations of \(\Vect{x} = (2,1)\).
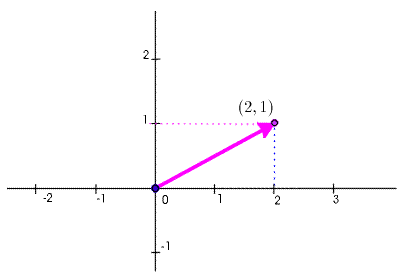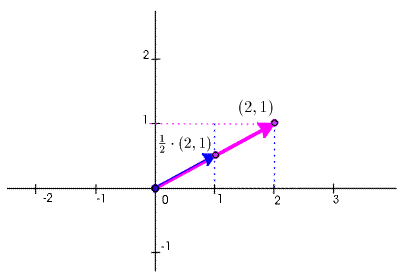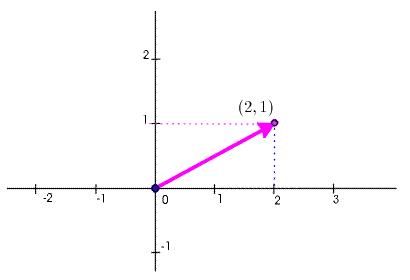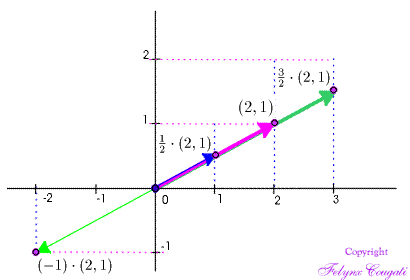
The linear combinations of a single vector \(\Vect{x}\) consist of all vectors of the form \(t\cdot \Vect{x}\), where \(t\) in \(\RNr\) is arbitrary. – The graphic below shows some linear combinations of \(\Vect{x} = (2,1)\).

We say that a vector \(\Vect{x}\) is a linear combination of two vectors \(\Vect{u}\) and \(\Vect{v}\) if there are numbers \(s\) and \(t\) in \(\RNr\) such that
| \(\Vect{x}\) | \(=\) | \(s \Vect{u} + t \Vect{v}\) |
Now if \(\Vect{x}\), \(\Vect{u}\), and \(\Vect{v}\) are given, The question arises: Are there numbers \(s\) and \(t\) so that \(\Vect{x} = s \Vect{u} + t \Vect{v}\)? and, if so, what are the possible choices of \(s\) and \(t\)? – In general, this question leads to a system of linear equations. The animation below illustrates this issue for the vectors
\[\Vect{u} = (-1,-1),\quad \Vect{v} = (2,1), \quad \text{and}\quad \Vect{x} = (1,-1)\]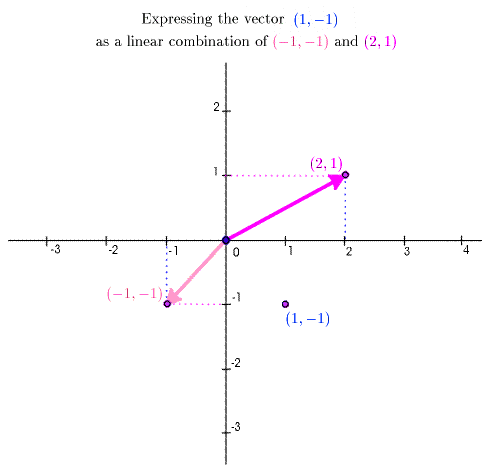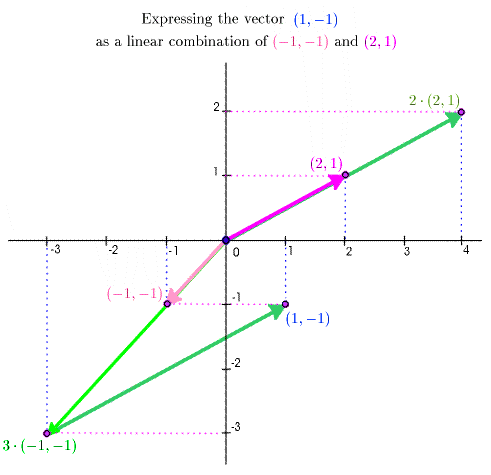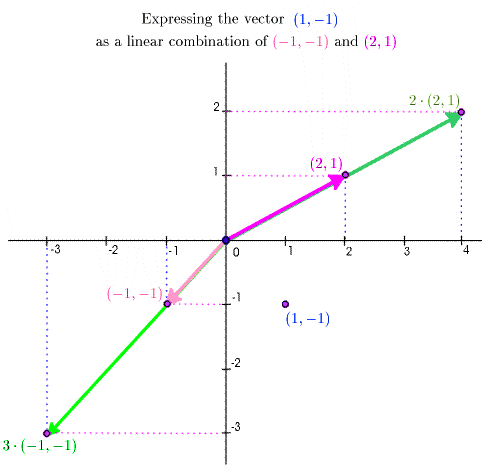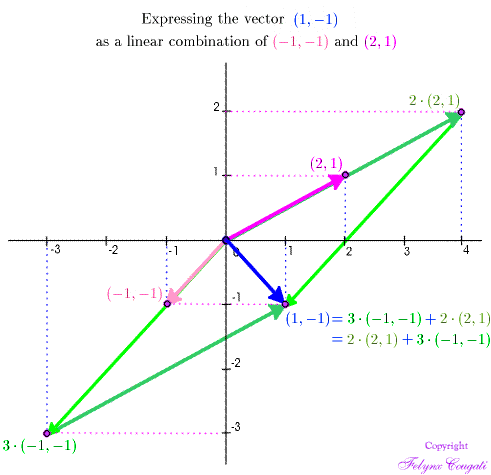
The animation goes through this progression:
This expression of \(\Vect{x}\) as a linear combination of \(\Vect{u}\) and \(\Vect{v}\) can be found formally as the unique solution of the system of linear equations
\[ \begin{array}{rcrcr} -s & + & 2t & = & 1 \\ -s & + & t & = & -1 \end{array} \]For another example of the previous type, let
\[\Vect{u} = (-1,-1),\quad \Vect{v} = (2,1), \quad \text{and}\quad \Vect{x} = (3,2)\]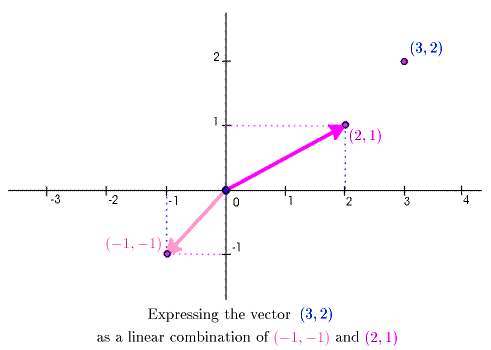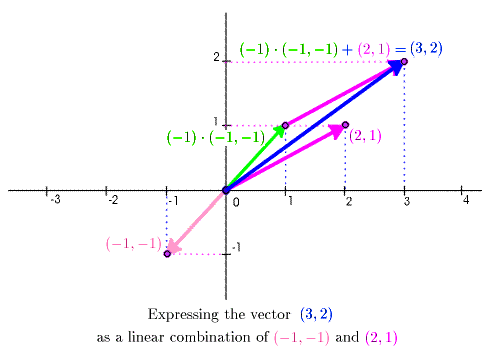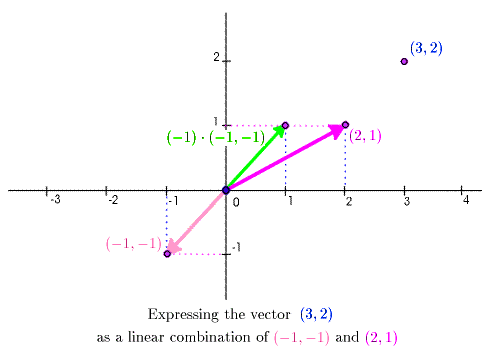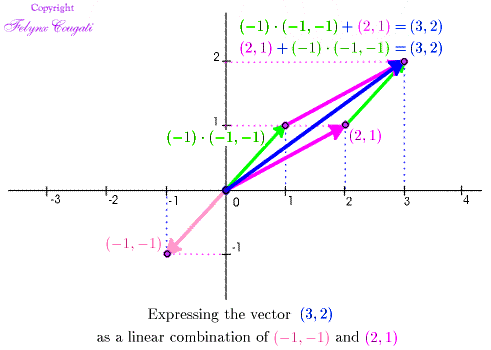
The animation goes through this progression:
This expression of \(\Vect{x}\) as a linear combination of \(\Vect{u}\) and \(\Vect{v}\) can be found formally as the unique solution of the system of linear equations
\[ \begin{array}{rcrcr} -s & + & 2t & = & 3 \\ -s & + & t & = & 2 \end{array} \]Any vector \(\Vect{x}=(x,y)\) in \(\RNrSpc{2}\) can be expressed uniquely as a linear combination of the vectors
\[\Vect{u} = (-1,-1)\quad \text{and} \quad \Vect{v} = (2,1)\]To express \(\Vect{x}\) as a linear combination of \(\Vect{u}\) and \(\Vect{v}\), we need to solve the system of linear equations
\[ \begin{array}{rcrcr} -s & + & 2t & = & x \\ -s & + & t & = & y \end{array} \]The coefficient matrix of the system if
\[ A = \left[ \begin{array}{rr} -1 & 2 \\ -1 & 1 \end{array} \right] \]which has \(\det(\Mtrx{A}) = 1\neq 0\). Therefore this system has a unique solution.
The animation below illustrates how to express the vector \(\Vect{x} = (2,1,2)\) of \(\RNrSpc{3}\) as a linear combination of the vectors.
\[\Vect{u} = (1,0,1/2)\quad \text{and} \quad \Vect{v} = (0,1,1).\]The animation goes through this progression:
With your mouse point to vectors which are linear combinations of \(\Vect{x}\).
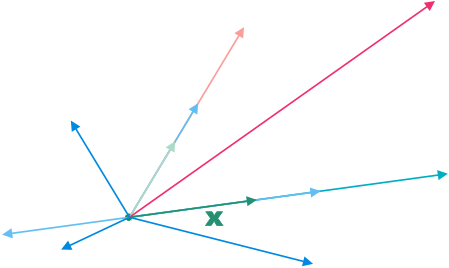
A linear combination of \(\Vect{x}\) is a vector of the form \(t\cdot \Vect{x}\), where \(t\) is in \(\RNr\). This means that a linear combination of \(\Vect{x}\) is any vector which is parallel to \(\Vect{x}\) or, in other words, which lies on the line in the direction of \(\Vect{x}\).
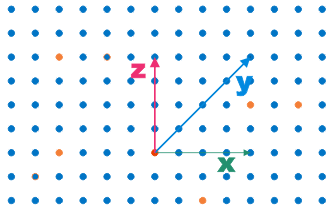
Express the position vector of each of the yellow dots as a linear combination of \(\mathbf{x}\), \(\mathbf{y}\), and \(\mathbf{z}\) in a least three distinct ways. – Place your mouse over top the point in question to find answers.