Proof
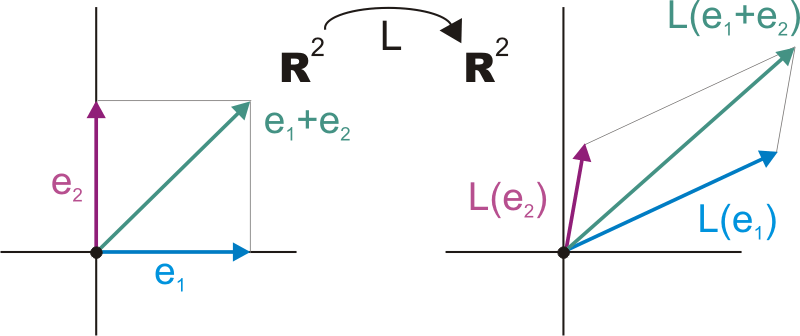
Our life here is made easy because, from the start, we are given the information that \(L\) is linear. So, we know that there is one and only one matrix which represents it: Its first column is given by the effect of \(L\) on the unit vector \(\StdBssVec{1}=(1,0)\), and its second column is given by the effect of \(L\) on the unit vector \(\StdBssVec{2}=(0,1)\) in the direction of the second coordinate axis.
| \(L(\StdBssVec{1})\) | \(= \) | \(L(1,0) = (3,1)\) |
| \(L(\StdBssVec{2})\) | \(= \) | \(L(0,1) = (1,2)\) |
Therefore the matrix representing \(L\) is
\[ A \DefEq \left[\begin{array}{cc} 3 & 1 \\ 1 & 2 \end{array}\right] \]This tells us that the unit square spanned by the vectors \(\StdBssVec{1}\) and \(\StdBssVec{2}\) gets transformed into the parallelogram spanned by the vectors \((3,1)\) and \((1,2)\).
Thus we see that \(L\) transforms the unit lattice of \(\RNrSpc{2}\) into the ‘slanted’ below.
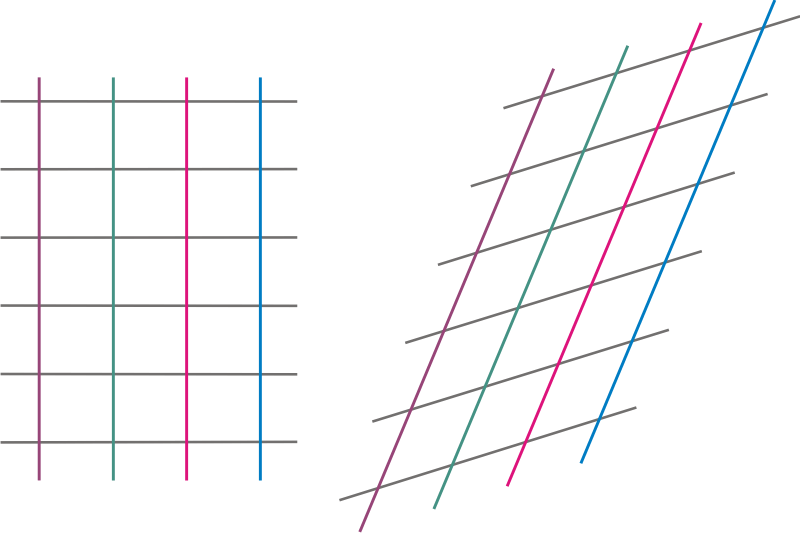
We now have two methods to compute how \(L\) transforms a specific point, say \(\Vect{x}=(2,5)\). We can either use the original definition of \(L\) and find
\[L(2,5) = (3\cdot 2 + 5 , 2 + 2\cdot 5) = (11,12)\]Alternatively, we can use the matrix \(\Mtrx{A}\) representing \(L\) to obtain
\[ L(2,5) = \left[\begin{array}{cc} 3 & 1 \\ 1 & 2 \end{array}\right] \left[\begin{array}{c} 2 \\ 5 \end{array}\right] = \left[\begin{array}{c} 3\cdot 2 + 5 \\ 2 + 2\cdot 5 \end{array}\right] = \left[\begin{array}{c} 11 \\ 12 \end{array}\right] \]