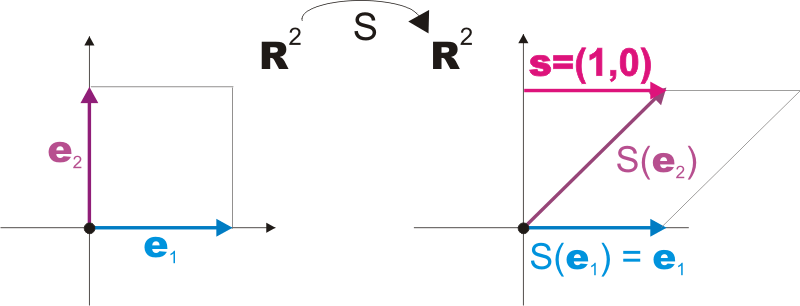
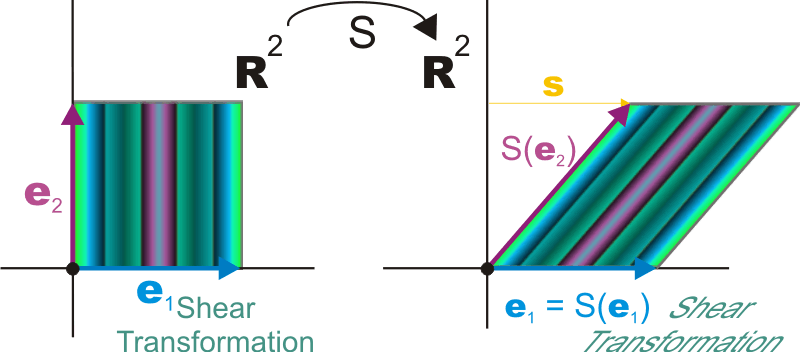
Example
The shear transformation \(S\) of \(\RNrSpc{2}\), parallel to the \(x\)-axis with shear vector \(\Vect{s} = (1,0)\) is given by.
\[ S\from \RNrSpc{2}\longrightarrow \RNrSpc{2},\qquad S(x,y) = \left[ \begin{array}{rr} 1 & 1 \\ 0 & 1 \end{array} \right] \left[ \begin{matrix}{c} x \\ y \end{matrix} \right] \]The transformation effect of \(S\) on the square spanned by the vectors \(\StdBss{1}\) and \(\StdBss{2}\) is illustrated in the image below.