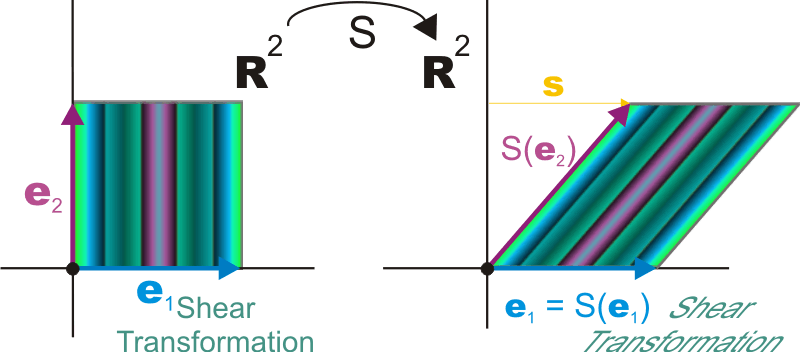
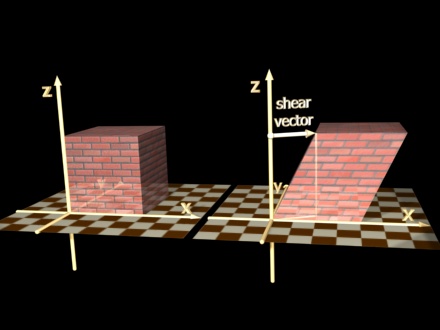
Solution
\(\Vect{n}\) is a unit vector. Therefore the shear vector is
\[\Vect{s} = S(\Vect{n}) - \Vect{n} = (1,1) - (0,1) = (1,0)\]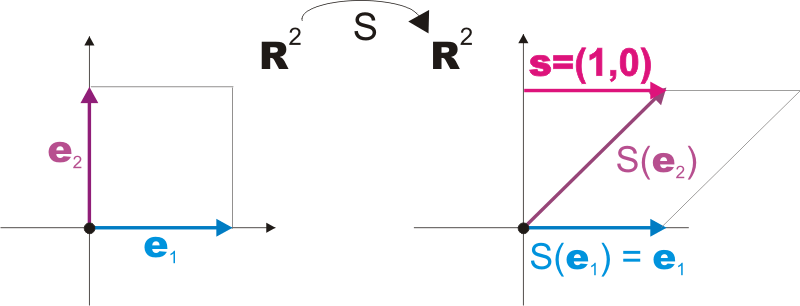
To find the matrix representing \(S\), we determine the effect of \(S\) on the vectors \(\StdBssVec{1}=(1,0)\) and \(\StdBssVec{2}=(0,1)\)
| \(S(1,0)\) | \(=\) | \((1,0) + \left( \DotPr{(1,0)}{(0,1)}\right) \cdot \Vect{s} = (1,0)\) |
| \(S(0,1)\) | \(=\) | \((1,1)\) |
Therefore,
\[ A = \left[ \begin{array}{rr} 1 & 1 \\ 0 & 1 \end{array} \right] \]