Here we explain how to compute the orthogonal projection of \(\RNrSpc{n}\) onto the hyperspace \(H\) which is perpendicular to a nonzero vector \(\Vect{a}\). We know that \(H\) consists of all those vectors \(\Vect{x}\) in \(\RNrSpc{n}\) with \(\DotPr{\Vect{a}}{\Vect{x}}=0\).
The orthogonal projection \(P\) of \(\RNrSpc{n}\) onto \(H\) transforms a point \(\Vect{x}\) in \(\RNrSpc{n}\) into the point \(P(\Vect{x})\) on \(H\) which is closest to \(\Vect{x}\). Intuitively, this may be viewed as follows:
- Shine a light perpendicularly onto \(H\).
- Then the orthogonal projection of a vector \(\Vect{x}\) onto \(H\) is the shadow of \(\Vect{x}\) on \(H\).
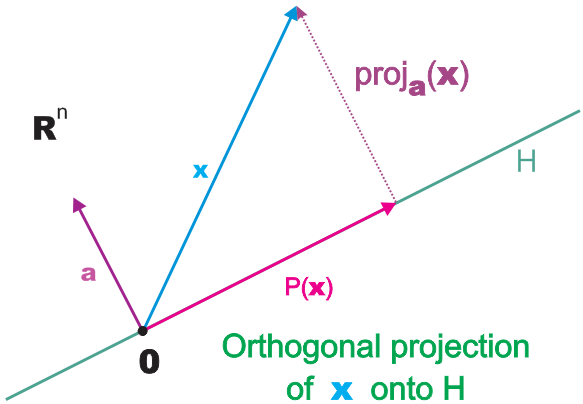
Thus we find \(P(\Vect{x})\) by subtracting from \(\Vect{x}\) the projection of \(\Vect{x}\) along \(\Vect{a}\).
\[P\from \RNrSpc{n} \longrightarrow \RNrSpc{n},\quad P(\Vect{x}) = \Vect{x}\ -\ \dfrac{\DotPr{\Vect{a}}{\Vect{x}}}{\DotPr{\Vect{a}}{\Vect{a}}} \cdot \Vect{a}\]