PropositionOrthogonal Projection of a Vector on a Line

Let \(\Vect{x}\) be an arbitrary vector of \(\RNrSpc{n}\), and let \(L\) be the line through the origin in the direction of a nonzero vector \(\Vect{y}\). Then the orthogonal projection of \(\Vect{x}\) onto \(L\) is the vector

\[\OrthoPrjctnOf{L}{\Vect{x}} = \dfrac{ \DotPr{\Vect{x}}{\Vect{y}} }{ \DotPr{\Vect{y}}{\Vect{y}} } \cdot \Vect{y}\]

Moreover, \(\Vect{y}\) is perpendicular to \(\Vect{x} - \OrthoPrjctnOf{L}{\Vect{x}}\).

Proof

We know that the projection vector has the direction of \(\Vect{y}\). So there is a number \(t\) with \(\OrthoPrjctnOf{L}{\Vect{x}} = \SclrPr{t}{\Vect{y}}\). For a given number \(t\), set

\(\Vect{u} \DefEq \Vect{x} - \SclrPr{t}{\Vect{y}}\) so that \(\Vect{x} = \SclrPr{t}{\Vect{y}} + \Vect{u}\).

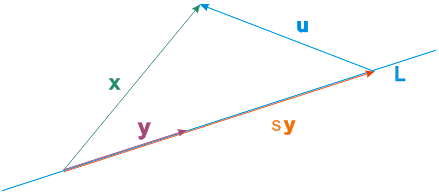
Then \(\Vect{u}\) is perpendicular to \(L\) if and only if \(\DotPr{\Vect{u}}{\Vect{y}} = 0\).

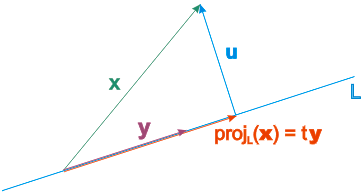
We find the number \(t\) for which this happens by dot producting both sides of the equation \(\Vect{x} = t\cdot \Vect{y} + \Vect{u}\) with \(\Vect{y}\):

\(\DotPr{ \Vect{x} }{ \Vect{y} }\)	\(=\)	\(\DotPr{ (t \Vect{y} + \Vect{u}) }{ \Vect{y} }\)
	\(=\)	\( \DotPr{ (t \Vect{y}) }{ \Vect{y} } + \DotPr{ \Vect{u} }{ \Vect{y} }\)
	\(=\)	\(t ( \DotPr{ \Vect{y} }{ \Vect{y} }) + 0\)
\(t\)	\(=\)	\(\dfrac{ \DotPr{ \Vect{x} }{ \Vect{y} } }{ \DotPr{ \Vect{y} }{ \Vect{y} } }\)

It remains to show that \(\OrthoPrjctnOf{L}{\Vect{x}}\) is perpendicular to \(\Vect{x} - \OrthoPrjctn{L}{\Vect{x}}\); i.e. we need to check that the dot product of the two vectors vanishes. So we compute

\(\DotPr{ \Vect{y} }{ (\Vect{x} - \OrthoPrjctnOf{L}{\Vect{x}}) }\)	\(=\)	\(\DotPr{ \Vect{y} }{ \left( \Vect{x} - \dfrac{ \DotPr{ \Vect{x} }{ \Vect{y} } }{ \DotPr{ \Vect{y} }{ \Vect{y} } }\cdot \Vect{y} \right) }\)
	\(=\)	\(\DotPr{ \Vect{y} }{ \Vect{x} } - \dfrac{ \DotPr{ \Vect{x} }{ \Vect{y} } }{ \DotPr{ \Vect{y} }{ \Vect{y} } }\cdot \DotPr{ \Vect{y} }{ \Vect{y} }\)
	\(=\)	\(\DotPr{ \Vect{y} }{ \Vect{x} } - \DotPr{ \Vect{x} }{ \Vect{y} }\)
	\(=\)	\(\DotPr{ \Vect{x} }{ \Vect{y} } - \DotPr{ \Vect{x} }{ \Vect{y} }\)
	\(=\)	\(0\)

So the two vectors in question are, indeed, perpendicular. – This completes the proof.